实验目的

理解卡方分析^[1]的原理，采用其攻击 Jsteg 算法^[2]，并验证 OutGuess 算法 ^[3]的改进。

原理说明

卡方分布

解释

卡方分布 ($\chi^2$分布)是概率论与统计学中常用的一种概率分布。$k$个独立的标准正态分布变量的平方和服从自由度为$k$的卡方分布。卡方分布常用于假设检验和置信区间的计算。

数学定义

若$k$个随机变量$z_1,z_2\cdots,z_k$相互独立，且数学期望为$0$，方差为$1$（即服从标准正态分布），则随机变量$X=\sum_{n=1}^kZ_n^2$服从自由度为$k$的的$\chi^2$分布，记作：

概率密度函数

卡方分布的概率密度函数$f_k(x)$为：

当$k\le0$时，$f_k(x)=0$

$\Gamma(x)$ 为伽马函数：

部分自由度下的密度分布函数

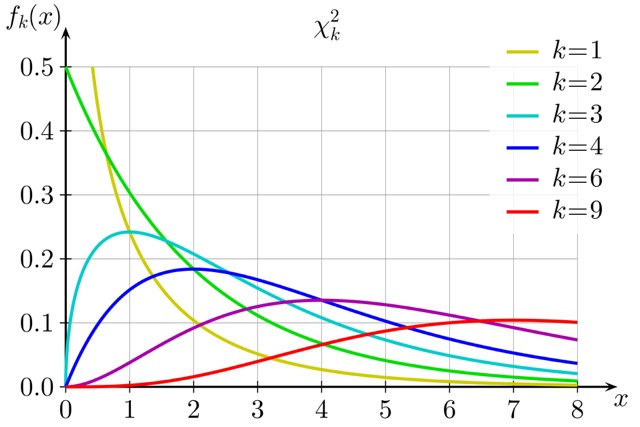
均值与方差

假设$\chi^2(k)$为自由度为$k$的卡方分布：

卡方分布表

下图 $p$ 越小置信度越高，分布约正常。

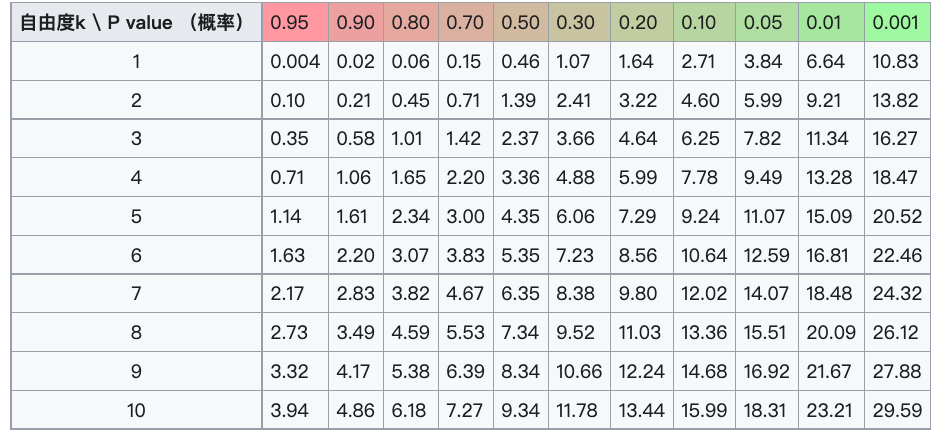
分析代码修改

根据提供的 $p$ 值提取算法进行了一定的修改，原分析的 $DCT$ 系数区间只能连续。

现将 $var$ 参数修改为要求输入一个偶数长度的数组，其两个一对，且要求每对之前的闭合区间长度为偶数。

function p = analysis(imgPath, var)
    jobj = jpeg_read(imgPath); % 图片读取
    zall = reshape(jobj.coef_arrays{1,1},1,size(jobj.coef_arrays{1,1},1)*size(jobj.coef_arrays{1,1},2));  
    % 连接好DCT系数

    z = zall;
    advh = [];
    len = length(var)/2;  % 计算有多少个区间
    for i = 1:len
        x = advh;
        y = histc(z,var(i*2-1):var(i*2)); % 计算每个区间内系数的出现次数
        advh = [x,y];   % 将所有区间计数结果拼接
    end

    pairnum = floor( length(advh) / 2);  % 计算值对总数
    t = length(advh);
    y = ones(pairnum,1);
    yy = ones(pairnum,1);
    for j = 1:1:pairnum
        if advh(2*j-1)+advh(2*j) > 0  
            y(j) = ( advh(2*j-1) + advh(2*j) ) / 2;  % 计算值对平均值
            yy(j) = max(advh(2*j-1),advh(2*j);  % 计算值对最大值
        else
            t = t - 2;   % 计算有效系数的数目
        end
    end
    xsq = sum( (y(:) - yy(:)).^ 2 ./ y(:) );  
    % (yy(j)-y(j))^2/y(j) 服从标准正态分布，则t/2有效值相加符合自由度为t/2卡方分布
    p = 1 - chi2cdf( xsq, t/2);
    % p越大越说明可能存在隐写，因为chi2cdf函数是从0到xsq积分（即正常的可能性）

实验步骤

1. 进行分析参数配置，设置卡方分析的量化 $DCT$ 系数检测区间;

   1. 根据基本原理，系数 $-1,0,1$ 三个系数不会被使用，DCT上限绝对值设置在 $1000$ 左右
   2. 对于正负两边，分别考虑其值对的对应情况
   3. 单边的DCT检测区间也是一个可以进行试验的目标
   4. 对于负数部分，设置 $DCT$ 检测区间 $[-1000,-3],[-999,-2]$，检测其负数值对的对应情况
   5. 对于正数部分，设置 $DCT$ 检测区间 $[2,999],[3,1000]$，检测其正数区间值对的对应情况
   6. 确定值对和范围后，联合正负区间进行验证
2. 攻击 Jsteg 算法，对于 Jsteg 算法产生的载体和隐写样本，计算它们的卡方分析值，验证卡方分析检测 LSB 类型隐写算法的有效性;
   1. $[-1000,-3]*****[-999,-2]$
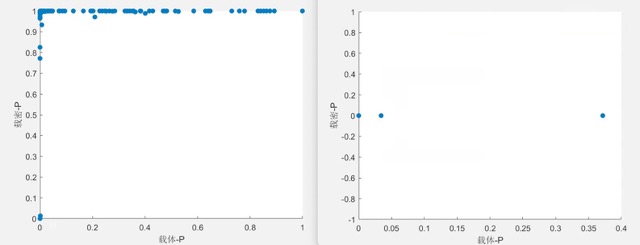
      由上面两个图可以发现在负值区左图有较好的鉴别能力，故负值区值对为$(-2i,-2i+1)$
   2. $[2,999]*****[3,1000]$
      由上面两个图可以发现在正值区左图有识别能力，故正值区值对为$(2i,2i-1)$
   3. 验证$[-1000,-3]\cup[2,999]$的分别效果
      
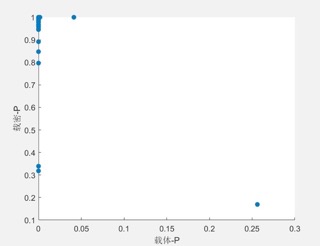
      在该种区间情况下，400个载体图片只有一个 $p$ 值为 $0.2992$，其它的全部为$0$，而载密载体图片$p$值全部非$0$，且大部分集中于$1$附近，达到了较好的区分效果

3. 攻击 OutGuess 算法，对于 OutGuess 算法产生的载体和隐写样本，计算它们的卡方分析值，验证 OutGuess 在安全性上的改进。

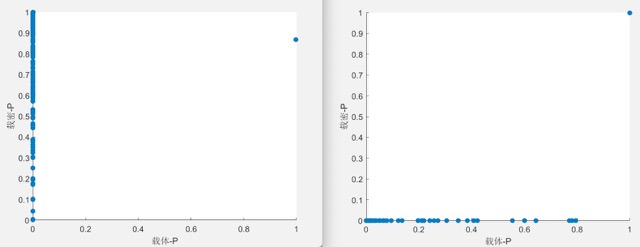
   1. $[-1000,-3]*****[-999,-2]$
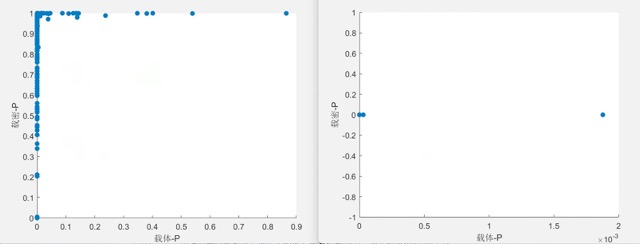
      由上面两个图可以发现在负值区左图有一定的鉴别能力，故负值区值对为$(-2i,-2i+1)$
   2. $[2,999]*****[3,1000]$
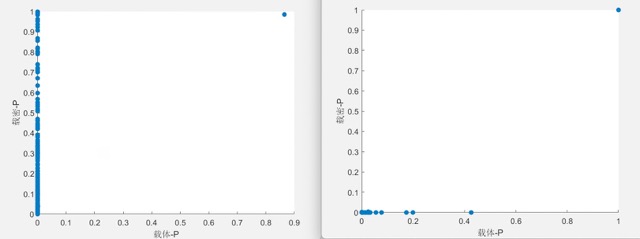
      由上面两个图可以发现在正值区左图有识别能力，故正值区值对为$(2i,2i-1)$
   3. 验证$[-1000,-3]\cup[2,999]$的分别效果
      
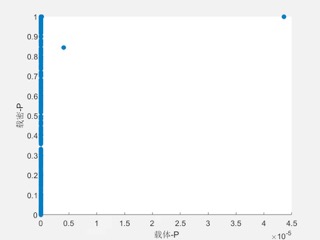
      在该种区间情况下，400个载体图片只有两个点 $p$ 值非0，其它的全部为$0$，而载密载体图片$p$值全部非$0$，且大部分集中于$1$附近，达到了一定的区分效果，但是没有Jsteg分辨能力强

实验要求

1. 实验报告必须包含对卡方分析的原理说明;
2. 实验报告必须包含详细的实验步骤描述，并配有相应的截图;
3. 实验报告必须详实记录具体的卡方分析配置参数，并通过散点图展示各个测试集的卡方分析结果;
4. 最终上传的压缩包中，除实验报告外，还应包含:实验过程中所编写的所有源代码。

实验提示

1. samples.rar 包含本次实验所需的全部样本，其中共有 4 个文件夹，文件 夹命名格式为“BOSS_StegoAlg_EmbedRate”，StegoAlg 表示算法名称，EmbedRate 代表嵌入率，例如，文件夹“BOSS_OTGS_500”包含的是采用 OutGuess 隐写算法，在0.5bpac 的嵌入率下制备的隐写样本;
2. 卡方分析的 matlab 函数接口为 p = analysis(imgPath, var)，其中，imgPath 表示待分析图像的路径，var 代表配置参数，其为结构体变量，成员包括 WinDown， WinUp，[WinDown, WinUp]表示进行卡方分析的量化 DCT 系数检测区间。

参考文献