主要内容
在视频上提出了一种新的隐写方法
- 第一次在视频上构造自适应量化
- 基于自适应量化提出了一种新的修改代价计算方法
- 提出了两种视频鲁棒隐写方法其相对于别的方法拥有更好的鲁棒性和安全性 (使用的变换不同)
前提
- 在YUV420的采样格式下,每个色度分量块 $Y_i$ ($32\times32$ 大小)都会有一个相应的色度分量块 $U_i$ ($16\times16$ 大小),它们共同表示画面的同一个区域。

- 文章描述 从色度分量块 $Y_i$ ($32\times32$ 大小)中经过 DTCWT-PCA 提取的特征 $x_i$ 与 从色度分量块 $U_i$ ($16\times16$ 大小)经过 DWT-SVD 提取的特征经过本地重压缩后的扰动$y_i$ 存在负相关关系。
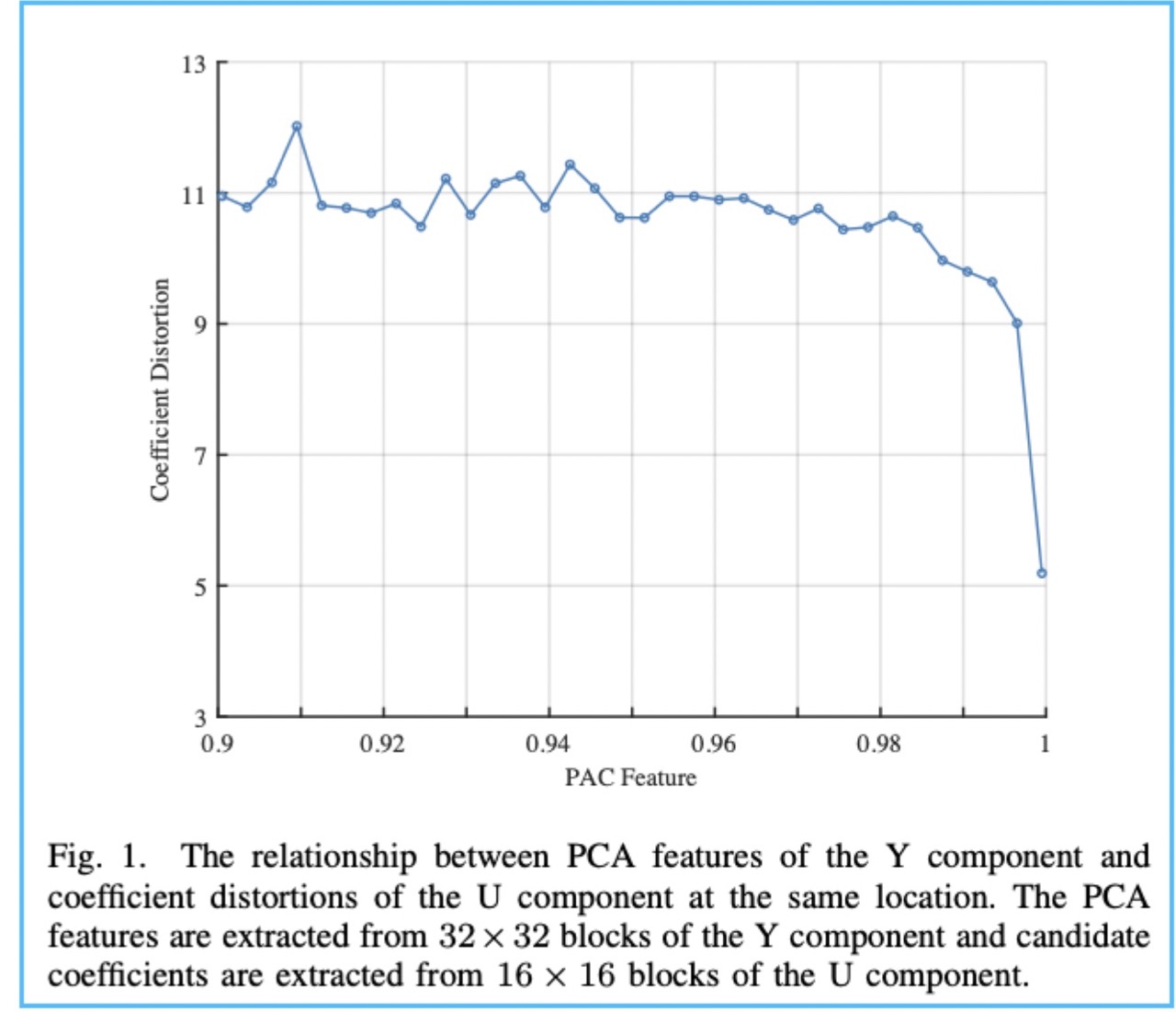
$Y_i(32\times32) \rightarrow x_i$:
- 对 $Y_i$ 进行 $DTCWT$ (双树复小波变换)会得到一个 $Y_i’$,然后对 $Y_i’$ 进行 $PCA$(主成分分析)后会有一个对角矩阵 $Λ = diag(λ_1, λ_2, …, λ_r, 0, …, 0)$
- $x_i = \lambda_1^2/\sum_{i=1}^r \lambda_i^2,0<x_i\le1$
$U_i(16\times16) \rightarrow y_i$:
- 对 $U_i$ 进行 $DWT$ (离散小波变换)会得到一个 $U_i’$,然后对 $U_i’$ 进行 $SVD$(奇异值分解)会有一个对角矩阵 $Λ = diag(λ_1, λ_2, …, λ_m, 0, …, 0)$
- 重压缩视频,会对 $U’_i$ 进行同样的操作,又会得到一个对角矩阵 $Λ’ = diag(λ’_1, λ’_2, …, λ’_n, 0, …, 0)$
- $y_i = \mid\lambda_1-\lambda_1’\mid$
整体嵌入流程
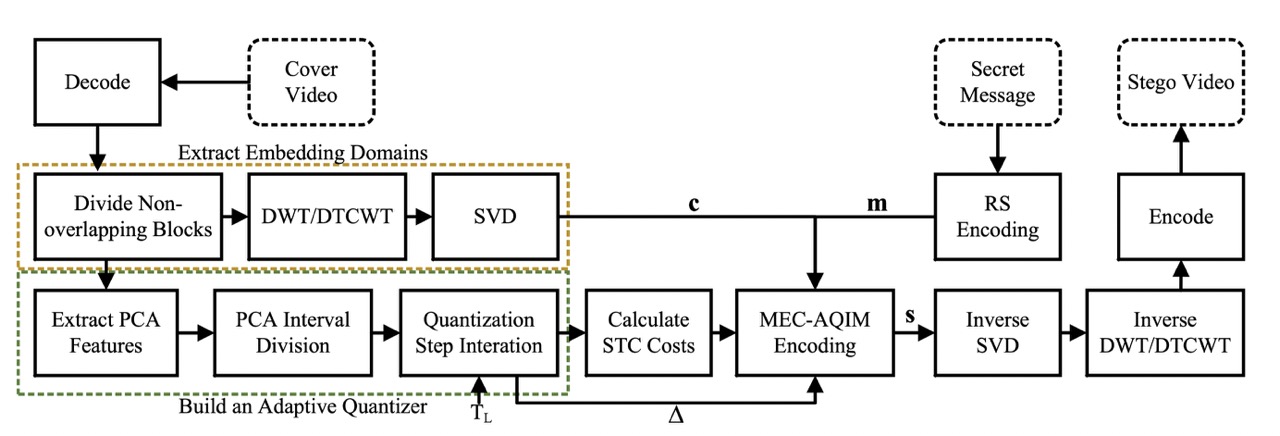
抽取嵌入域
嵌入域从色度分量U中提出
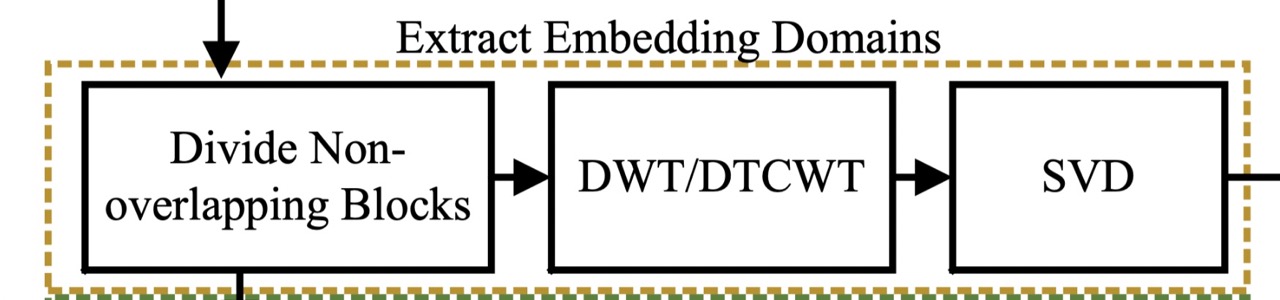
- 将色度分量U分成大小为$16\times16$ 并且互不相交的块
- 对每一个块 $U_i$ 进行 $DWT$ (离散小波变换)会得到一个 $U_i’$,然后对 $U_i’$ 进行 $SVD$(奇异值分解)会有一个对角矩阵 $Λ = diag(λ_1, λ_2, …, λ_m, 0, …, 0)$,每个块会得到一个特征值 $c$,且$c = \lambda_1$
- 将所有块的 $c$ 按顺序连接起来久得到了嵌入域 $C$
期间使用的 $DWT$(离散小波变换)也可以换成 $DTCWT$(双树复小波变换),别的环节不变,这个地方也就是文中所提的两种方法唯一的不同之处。
自适应量化
自适应量化参数基于 $Y$ 和 $U$ 组件的信息产生

初始划分
同前面的负相关关系,从一个亮度空间块 $Y_i(32 \times 32)$ 可以提取出一个特征值 $x_i$
- 对 $Y_i$ 进行 $DTCWT$ (双树复小波变换)会得到一个 $Y_i’$,然后对 $Y_i’$ 进行PCA(主成分分析)后会有一个对角矩阵 $Λ = diag(λ_1, λ_2, …, λ_r, 0, …, 0)$
- $x_i = \lambda_1^2/\sum_{i=1}^r \lambda_i^2,0<x_i\le1$
现使用 $p_i$ 表示特征值 $x_i$,$0<p_i\le1$,由于$p_i$是连续的,可以用区间将 $p_i$ 划分成105个单元。
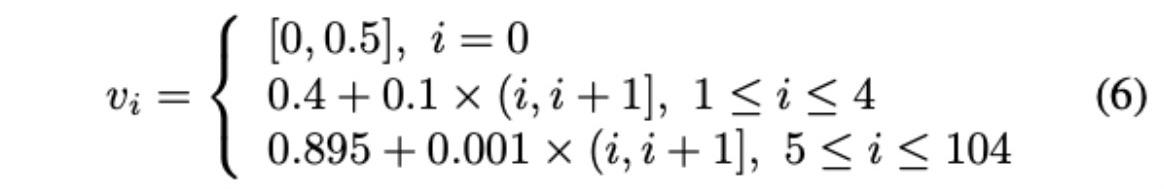
这样划分的原因是主成分分析后 $p_i$ 大部分集中于 $[0.9,1)$ 区间。
贪心合并
由于视频在重压缩后可能导致有些块的特征值跳入邻近的单元,现通过贪心算法再次合并单元减少跳入其它单元的情况。
- 对于一个视频,计算亮度空间 $Y$ 每个块重压缩前和压缩后的 $p$ 和 $p^*$。若 $p \in v_i$,$p^* \in v_j$,且 $i\not=j$,则有一个错误出现在了第 $i$ 个单元。统计每个单元内出现的错误数量,得到 $E = \lbrace E_1,E_2,\cdots,E_{105} \rbrace$
- 建立一个宽度为 $w$ 的滑动窗口,逆序遍历 $E$
- 假设当前窗口的起点为 $a$,则当前包含的单元区间为 $\lbrace E_{a-w+1},E_{a-w+2},\cdots,E_a\rbrace$,找到其中最小 $E_b,b\in [a-w+1,a]$,将 $\lbrace E_b,E_{b+1},\cdots,E_a \rbrace$ 合并成一个区间 $m$,设置新的窗口起点为 $b-1$
- 重复第3步,直到所有单元被包含在新的区间,得到新的划分方式 $M=\lbrace m_1,m_2,\cdots,m_t\rbrace$
量化步长分配
- 通过上述初始化分及贪心合并,亮度空间 $Y$ 中所有的块依据划分方式 $M$ 被分在了 $t$ 个不同的集合当中。
- 依据亮度空间 $Y$ 的块与色度空间 $U$ 的块的一一对应性,则色度空间 $U$ 的所有块也被划分在 $t$ 个不同的集合当中。
- 在同一个集合中的色度空间块其特征值将使用相同的量化步长进行量化
接下来说明如何求得这 $t$ 个集合各自的量化步长 $\delta$
对于每个集合
- 首先初始化最小量化步长 $\delta^{min}$ 和最大量化步 $\delta^{max}$
- 计算 $\delta^{arg} = (\delta^{min}+\delta^{max})/2$,对同一个集合中的色度空间块SVD特征 $C_i$ 使用 $\delta^{arg}$ 量化得到 $C_i^q$,将视频的 $C_i$ 换成 $C_i^q$,构造新的视频
- 有损重压缩视频并提取相同位置的色度空间块SVD特征到 $C_i^{q*}$
- 遍历集合中每个元素,每当$\mid c_i^q-c_i^{q*}\mid>\delta^{arg}/2$,错误数目加$1$,得到最终的错误数目总和 $e_i$
- 设定阈值$\tau$,当 $e_i<\tau$时,令$\delta^{max}=\delta^{arg}$,否则令$\delta^{min}=\delta^{arg}$
- 重复步骤2至步骤5,直到$\delta^{min}=\delta^{max}$,由此得到第$i$个集合的量化步长 $\delta_i=\delta^{min}=\delta^{max}$
由上述方法,基于阈值$\tau$,可以得到各个集合的量化步长集合$Q=\lbrace\delta_1,\delta_2,\cdots,\delta_t \rbrace$
量化
\[idc_i = \lfloor c_i/\delta_i +0.5 \rfloor \tag1\] \[c_i^q = idc_i\cdot\delta_i \tag2\] \[x_i=idc_i \pmod2 \tag3\]其中$c_i$为色度分量块$u_i$的$SVD$特征值,$\delta_i$为块$u_i$所在集合的量化步长,$C_i^q$为$c_i$量化后的值,$x_i$为$c_i$量化后对应的二进制比特
\(ids_i = \begin{cases} idc_i+(idc_i+y_i)mod\ 2, c_i^q<c_i \\ idc_i-(idc_i+y_i)mod\ 2, c_i^q\ge c_i \end{cases} \tag 4\) 其中$X={x_1,x_2,\cdots,x_n}$是原载体比特串,$Y={y_1,y_2,\cdots,y_n}$是要写入的比特串。
当扰动相同时,块越稳定,所需量化步长越小。因为块越稳定,重压缩后特征值变化的幅度就越小。
嵌入代价计算
使用$STC$编码时候需要计算 $cost$,文章将这个 $cost$ 分成了两个部分
当载体$SVD$特征系数$c_i$被转换为隐写$SVD$特征系数$s_i$时,因为使用了量化的方法,那么这个过程可以计算出一个量化的修改代价记为$\rho_{d,i}(c_i,s_i)$。 除此之外,既然是鲁棒性算法,那个鲁棒程度也可以存在一个鲁棒程度代价,记录为$\rho_{r,i}(c_i,s_i)$。
鲁棒性代价:$\rho_{r,i}(c_i,s_i)=\delta_i$,其中$\delta_i$为$c_i$对应的色度空间块$U_i$所在集合的量化步长
量化代价:
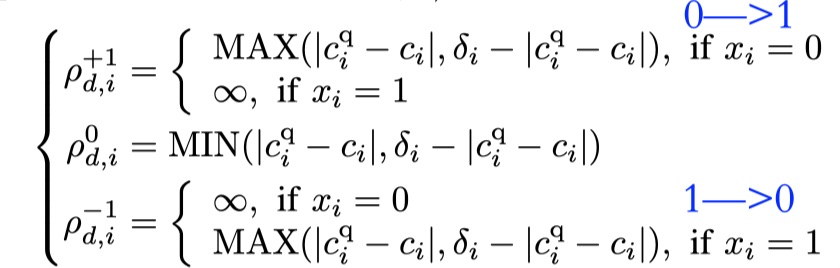
结合上面的两个代价,得到最终代价,就是两者相乘
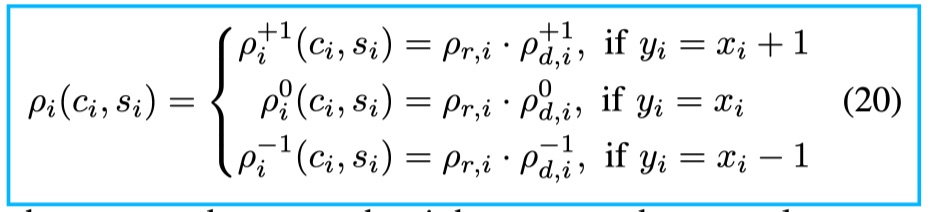
汇总
色度空间 $Y={Y_1,Y_2,\cdots,Y_n}$, 亮度空间$U={U_1,U_2,\cdots,U_n}$
- 每个色度空间块$Y_i$可以提取出一个PCA特征 $p_i=F_{dtcwt-pca}(Y_i)$,每个亮度空间块$U_i$可以提取出一个SVD特征 $c_i=F_{dwt-svd}(U_i)$
- PCA特征集$P={p_1,p_2,\cdots,p_n}$的特征值都属于 $[0,1)$,可以被划分在$105$个连续的区间中,经过贪心和在一个重压缩通道$T_c$下并可以把 $105$ 个区间合并为$t$个连续的区间集合$M={m_1,m_2,\cdots,m_t}=F_{merge}(P,T_c)$。SVD特征集$C$与PCA特征集$P$中的元素是一一对应的关系,则SVD特征集$C$所有元素会被划分在$t$个单元当中。
- 利用二分算法,在阈值$\tau$和有损通道$T_c$下,属于$t$个不同单元的SVD特征集$C$会求得其各自的量化步长$Q={\delta_1,\delta_2,\cdots,\delta_t}=F_{binary}(C,Q,T_c,\tau)$
- 在第4步后,每个SVD特征集$C$中的元素有其对应的量化步长,可以得到载体比特串$c=F_{q}(C,Q)$
- 载体比特串元素的嵌入代价可以由SVD特征集$C$和量化步长$Q$得出,$COST=F_{cost}(C,Q)$
- 初始信息经过纠错码编码可以得到消息比特串$m$,接下来就可以进行STC嵌入了,得到与载体比特串$c$等长的密文比特串$s=STC(c,m,COST,w,h)$
- 将 $c$ 换成 $s$,随后进行$F_{dwt-svd}^{-1}$,就是把这个特征逆变换成初始的系数,完成后续编码得到载密视频。
提取
- 提取需要接收方得到同视频的划分方式 $M=\lbrace m_1,m_2,\cdots,m_t\rbrace$和量化步长集合$Q=\lbrace\delta_1,\delta_2,\cdots,\delta_t \rbrace$,共$2t$个值。
- 同嵌入时的操作方法,将色度分量块$Y$分成$32\times32$ 大小的块,将色度分量块$U$分成$16\times16$大小块,这些块一一对应且数量相等。
- 提取每个色度分量块$Y_i$的 $DTCWT-PCA$ 特征值 $p_i$。根据划分方式$M$,便可以得到与$Y_i$对应的色度分量块$U_i$提取出的$DWT-SVD/DTCWT-SVD$特征值$c_i$的量化步长$\delta_i$
- 对所有块对$(Y_i,U_i)$求出对应量化步长后,解量化就可以得到二进制载密串$s$
- 对$s$使用编码过程中相同设置进行STC解码,RS解码,得到最终消息
实验结果
BCH纠错码
- $BCH(n,k)$
- 满嵌入时候相当于实际的负载率$e = k/n$
- BER错误率,最终选择了$n=127,k=63$
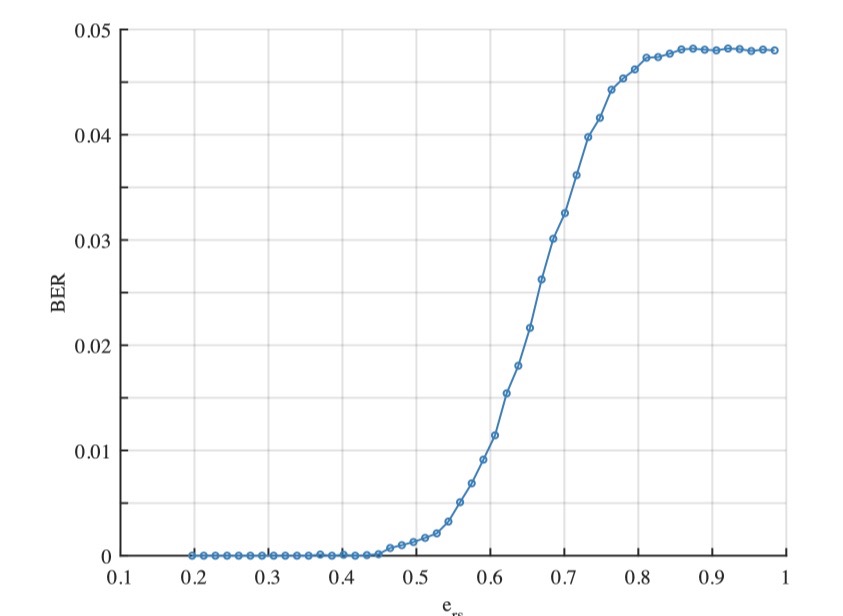
重压缩通道设置
一共设置了八种重压缩的通道
- CRF(固定速率系数,Constant Rate Factor)
- QP(量化参数,Quantization Parameter)
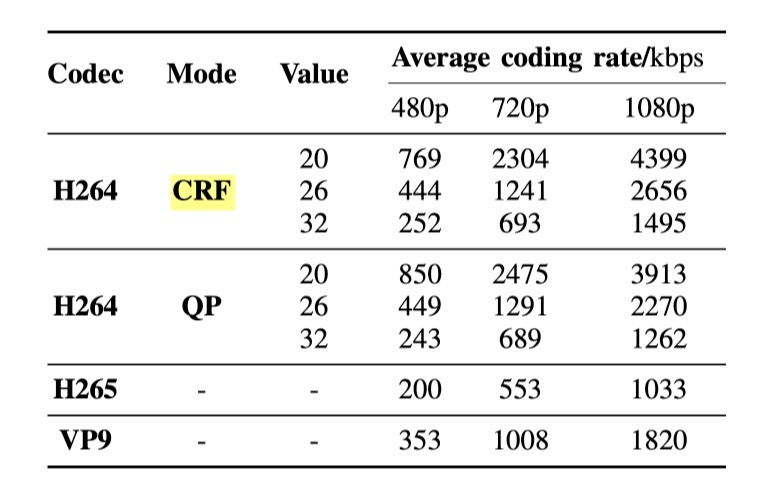
评价指标
- $c_i$ 嵌入前的系数
- $s_i$ 嵌入后的系数
- $s_i^*$ 重压缩后的系数
- $n$ 嵌入过程中改动的系数总数量
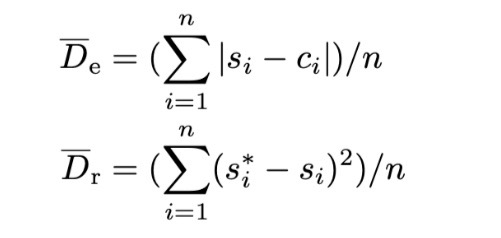
四种嵌入方式
- QIM: 不使用STC,基本的量化嵌入方式,固定所有量化步长为$q=\sum_{i=1}^t\delta_i/t$
- AQIM: 不使用STC,使用自适应量化步长$Q=\lbrace\delta_1,\delta_2,\cdots,\delta_t \rbrace$
- MEC_AQIM/-STC: 使用STC,所有载体代价全部相同,使用自适应量化步长。
- MEC_AQIM: 使用STC,所有载体代价独立计算,使用自适应量化步长
扰动部分结果
$\overline{D_e}$的实验结果
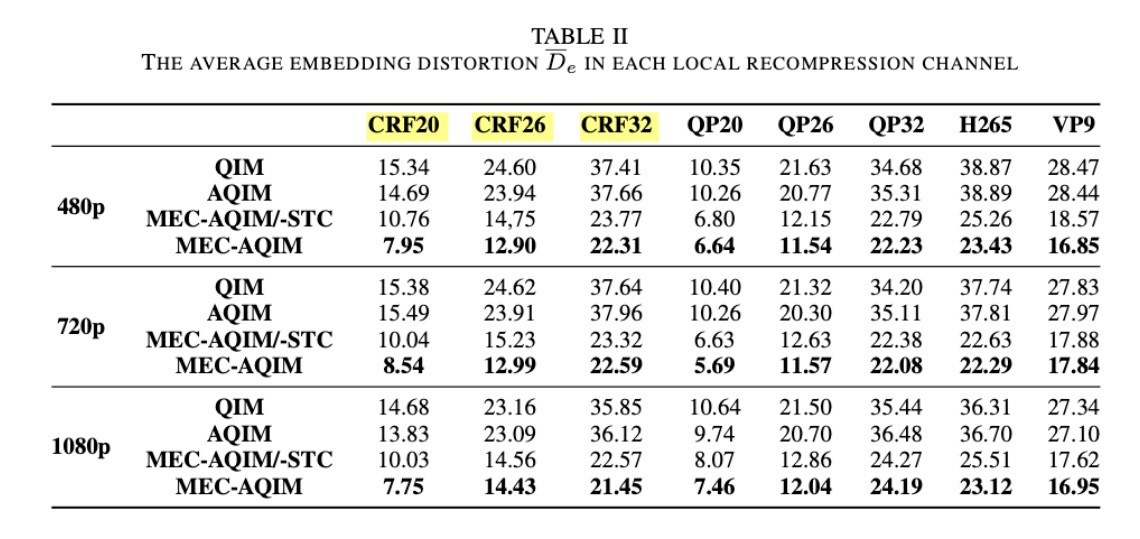
$\overline{D_r}$的实验结果
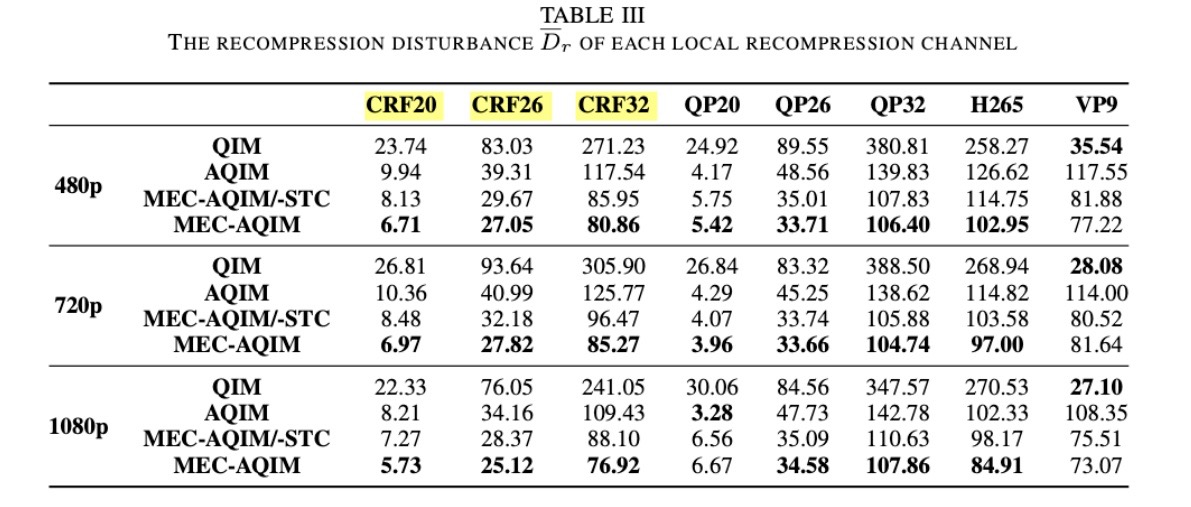
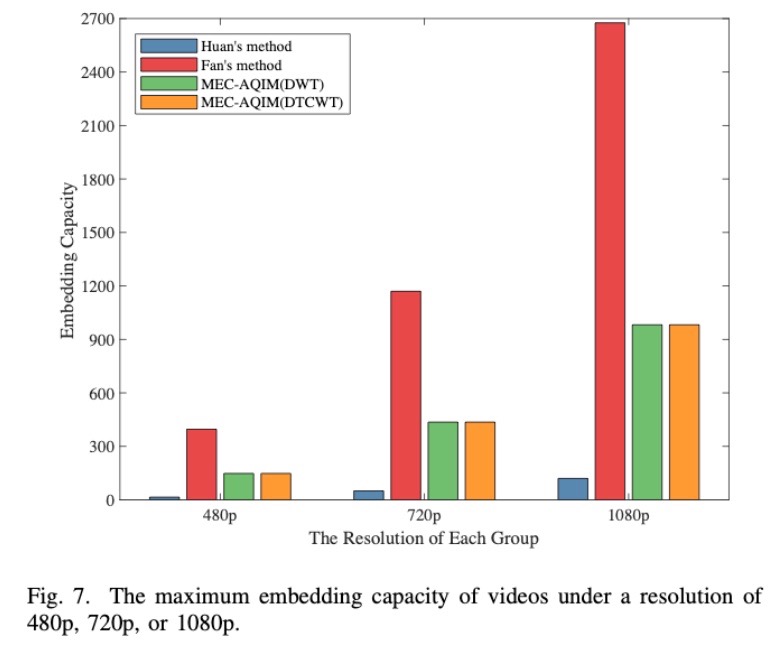
嵌入容量
Fan’s method 比MEC-AQIM好,是因为 Fan’s method是在$Y$组件中嵌入。在视频是YUV420格式下,$Y$组件将可以获得四倍的嵌入容量相当于$U$组件。
在$U$组件中嵌入可以在容量和可见性之间达到一个均衡。
 </div>
</div>
鲁棒性
并不是所有方法都使用了纠错码,所以首先设置了两个误码率
- $R_{e1}$ 表示的是STC解码之后纠错码解码之前的误码率
- $R_{e2}$ 表示最终消息比特串的误码率
假设视频数量是 $g$,可以衍生出两个错误率 $\overline{R_{e1}}$ 和$R_s$
- $\overline{R_{e1}}=\frac1g\sum_{i=1}^gR_{e1}(i)$,即$\overline{R_{e1}}$代表STC解码之后纠错码解码之前$g$个视频的平均误码率
- $R_s=\frac1g\sum_{i=1}^g\delta(R_{e2}(i))$,其中$\delta(\circ)$表示$\circ$为0时值为1,其它情况为0,即$R_s$代表完整传输消息的成功率
本地
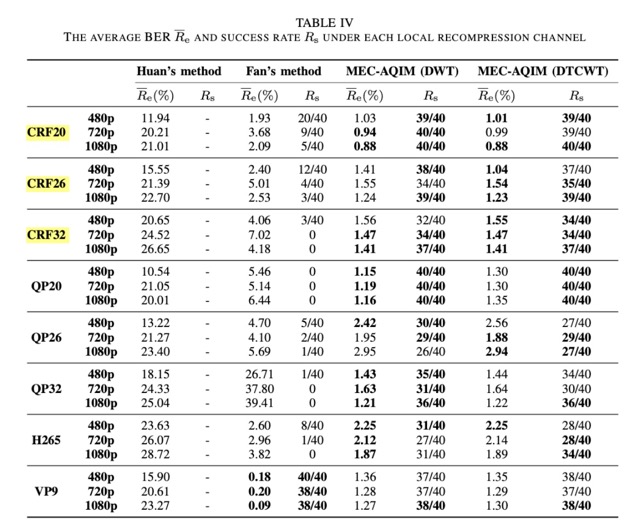
流媒体
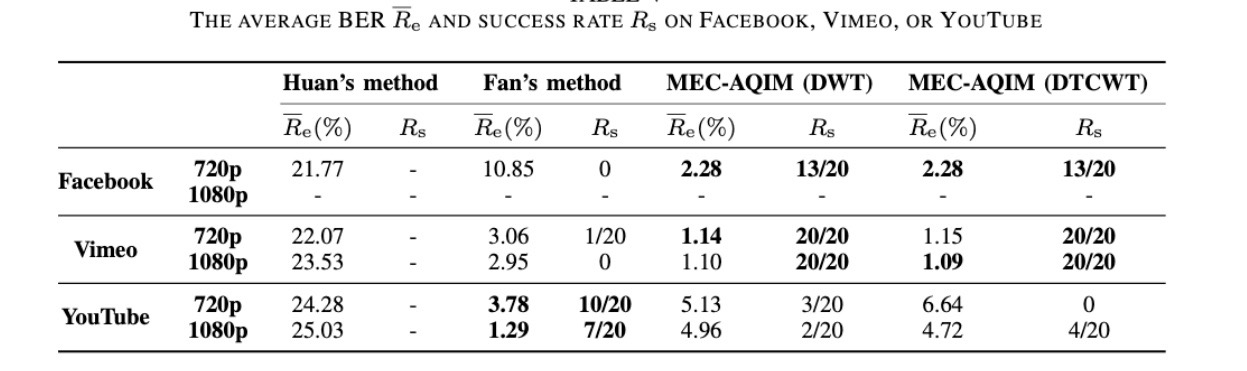
安全性
训练集由50%随机选择的cover和stego对组成,测试集由剩余的50%cover和stego对组成。
- $P_E = \min_{P_{FA}}\cfrac{1}{2}(P_{FA}+P_{MD})$
- $P_{FA}$表示把cover识别成stego的概率(错检)
- $P_{MD}$表示把stego识别成cover的概率(漏检)
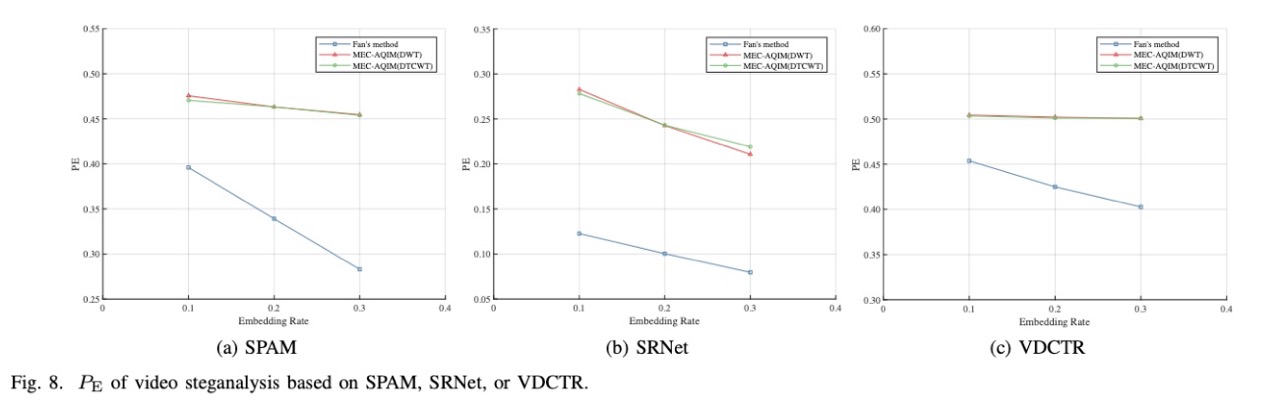
视觉逼真度(Visual fidelity)
PSNR(Peak Signal-to-Noise Ratio,峰值信号比) 和 SSIM(Structural SIMilarity,建构简单性) 指标
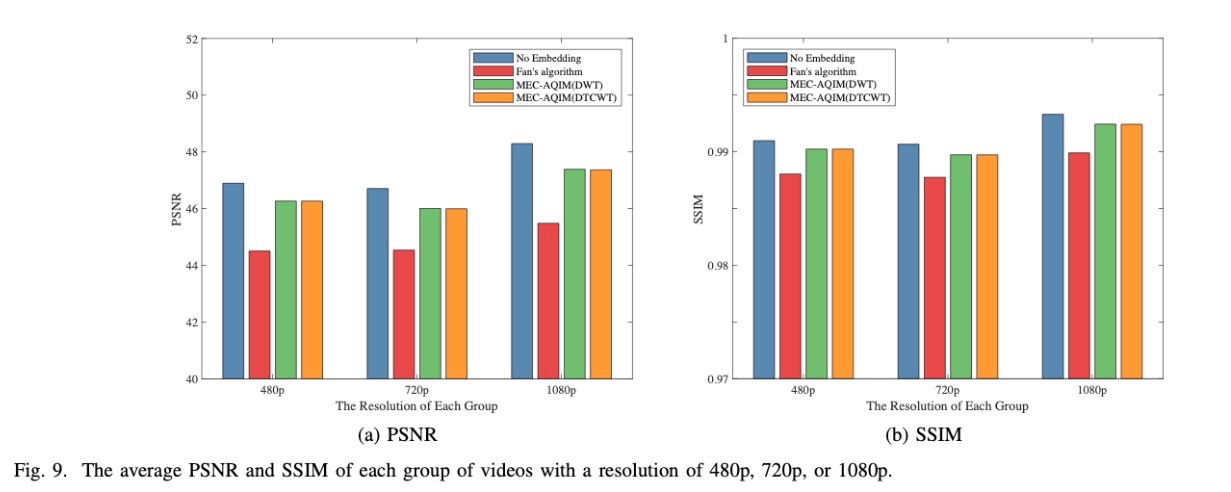
文档信息
- 本文作者:Jiamin Zeng
- 本文链接:https://jiaminzeng.github.io/2022/10/25/Paper-%E8%A7%86%E9%A2%91%E9%9A%90%E5%86%99/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)