1. 原文章
A Robust MP3 Steganographic Method against Multiple Compressions Based on Modified Discrete Cosine Transform
提出了一种针对 $\text{mp3}$ 的 $\text{MDCT}$ 系数域鲁棒性的音频隐写算法
1.1 文章发现
1.1.1 能量变化
$\text{mp3}$ 每一帧有两个颗粒,每个颗粒可以有四种块,其有着对应的的比例因子带使用情况。
- 一个一般长块( $21$ 个比例因子带)
- 一个起始长块( $21$ 个比例因子带)
- 一个终止长块( $21$ 个比例因子带)
- 三个短块(不混合:$12\times3$ 个比例因子带;混合:$(8+4)\times3$ 个比例因子带,$[0,7]long,[3,5]short$)
能量最大的几个比例因子带在经历过 $5$ 次重压缩之后,能量大小分布仍然基本保持。
随机选了一个音频的第一帧进行两种码率的尝试。
1.1.2 最大幅度位置
一个比例因子带中有多个频谱系数 ($\text{MDCT}$ 系数),其中会有一个最大的值(其实也可能多个,先假设一个吧)。
那么这个最大值的位置在重压缩后是可能修改了的。
文章给了一个音频的 $100$ 帧的重压缩后最大位置的坐标变动情况(经过了 $5$ 次重压缩)
这里得出了一个结论就是能量高的频带,最大幅度的 $\text{MDCT}$ 系数所在位置变化不大
1.2 嵌入与提取方法
1.2.1 嵌入
- $\text{BCH}$ 对比特消息流置乱。
- 对于每一个颗粒根据频带的划分情况,长块 $21$ 个比例因子带,短快 $36$ 个比例因子带,计算每一个频带的平均能量。 \(e_i=\cfrac{1}{n}\sum_{i=1}^n(x_i)^2\)
- 每个颗粒中选择出能量前 $k$ 大的频带用于嵌入,一个频带嵌入一个比特。
- 假设这个频带有 $4$ 个MDCT值,其 绝对值 是 $[0.02,0.01,0.08,0.9]$,位置分别是 $[0,1,2,3]$。
- 偶数位是 $[0.02,0.08]$,奇数位是 $[0.01,0.09]$,最大的值是 $0.09$ 在奇数位,所以这个频带表示的比特是 $1$。
- 假如恰好满足就不用修改了,如果不满足那么就要进行修改。
- 修改策略,先求出左边和右边最大值的差值的 $sub = \mid 0.8-0.9 \mid =0.1$,然后 $0.8+\alpha\cdot sub,0.9-\beta\cdot sub$。$\alpha=\beta=1$ 时就是互换,这样满足了嵌入的要求。
- 对每一个颗粒重复 $2$ 和 $3$ 直到所有比特嵌入完成
每个颗粒可以嵌入 $k$ 个, $k$ 取小于5。
1.2.2 提取
执行下步骤 $2,3$,再 $BCH$ 逆一下。(置乱)
1.3 嵌入容量
\[\cfrac{4\times k \times R}{1152} \ \ \ (bit/s)\]$k$ 是取前多少个,$R$ 是采样率。($R=44.1\text{kHz}$)
1.4 试验结果
1.4.3 统计不可检测
$\text{MDI2}$ 和 $\text{JPBC}$,被识别准确率都在 $\%55$ 左右
2. 在 $\text{lame}$ 上的实现
2.1 长短块
实现的时候对所有比例因子都采用了长块的划分方式,现在看来应该得已经长短块情况划分不同的比例因子带。
重压缩时候一旦有一个颗粒发生比例因子带的变化,那么这个颗粒嵌入的肯定无法准确被提取。
(2.1) 如果处理长短在重压缩时候的变换导致的提取错误?
2.2 嵌入方式
一个数量为 $4$ 的比例因子带,其值分别为 $[a_0,a_1,a_2,a_3]$,偶数位有 $[a_0,a_2]$,奇数位有 $[a_1,a_3]$。
偶数位中最大的为 $a_0$,奇数位中最大的为 $a_1$
- 极端情况下 $a_0 = a_1$,$sub=\mid a_0-a_1\mid = 0$。
- 假设整个比例因子带的时候是从小到大寻找,那么 $a_0$ 会先出现,那么这个比例因子带表达的就是比特 $0$。
- 但是如果要嵌入比特 $1$,执行之前的修改策略就是 $a_0=a_0-\alpha\times sub,a_1=a_1+a_1\beta\times sub$
如果差值不大的话,量化会使得修改无效
实现的时候加上了常数 $eps$, $a_0=a_0-\alpha\times sub-eps,a_1=a_1+a_1\beta\times sub+eps$
(2.2) 在这种直接修改MDCT系数的方法下控制好修改幅度是很困难的,幅度如果修改比较恰当?
2.3 静音帧(最大的困扰)
- 如果嵌入,只能依赖常数,扰动很大
- 不嵌入,就会涉及到帧的筛选
(2.3) 如果处理静音帧?
2.4 试验结果
试验时静音帧也进行了嵌入。
首先就是文章的方法,$\alpha = \beta= 1.1$,试验的结果大概是 $5\%$ 左右的错误率,然后遇到静音多的音频效果特别差。
然后加上 $eps$,效果会变好然后在 $eps$ 取 $0.001,\alpha = \beta= 1.2$ 错误率在 $1.3\%$ 左右,后面测试加 $\text{BCH}$ 可以降到 $1\%$ 以下,噪音有点杂。
3. 算法迁移至 $\text{AAC}$
3.1 嵌入方法
3.1.1 嵌入域和基本修改方式
$2.2$ 解决方案
最理想的修改方式就是使得 比例因子带内最大的 $\text{MDCT}$系数 在量化后恰好比别的幅度都大 $1$ 。
一个简单达到该目的的方式就是直接修改 $\text{QMDCT}$ 系数,这在 $\text{lame}$ 的编码过程中不允许,但是 $\text{faac}$ 编码过程中可以修改。
那么就同 $\text{mp3}$ 的嵌入提取方法,在 $\text{QMDCT}$的频带实现之前的嵌入方法。
不过要修改策略稍微修改了一下
比例因子带选择
$\text{44.1kHz}$ 采样率下长块共有 $49$ 个比例因子带。
- $[0,9]$ 宽度为 $4$
- $[10,16]$ 宽度为 $8$
- 剩下的至少为 $12$,后面越来越宽
选择前 $[0,16]$ 频带进行嵌入,共 $17$ 个
$(3.1)$ $1024$个点的 $\text{MDCT}$ 变换。如果不是静音帧,低频肯定有值? (稍微试验了一下)
幅度修改
- 假设奇数位幅度最大的值为 $a_{old}$,偶数位幅度最大的值为 $a_{even}$
- $a_{old}<a_{even}$,要嵌入 $1$,$a_{old}=a_{even}+2,a_{even}=a_{old}$
- $a_{old}>a_{even}$,要嵌入 $1$,$a_{old}=a_{old}+1$
- $a_{old}=a_{even}$,嵌入 $1$:$a_{old} = a_{old}+2$;嵌入 $0$:$a_{even} = a_{even}+2$
$(3.2)$ 可行,但是还是可以进行试验探讨。有很小的可能造成幅度溢出。
3.1.2 长短块问题解决方案
$(2.1)$ 解决方案
- $\text{AAC}$ 有长短窗,且短窗会被分组。
- 重压缩会导致短窗分组情况会变化,长短之间会产生一定数量的切换。
$\text{faac}$ 编码的时候有一个比较特殊的参数,利用这个参数便可以在 $\text{wav}\Rightarrow \text{acc}$ 编码时候全部都是 长窗或者短窗
--shortctl X Enforce block type
X (0 = both (default); 1 = no short; 2 = no long).
(短块未尝试)
嵌入提取过程:

3.1.3 $\text{faac_s}$ 编码过程优化
上述嵌入提取过程,可以有一个很巧妙的对等
因为如果只使用长窗变换,且先忽略 $\text{AAC}$ 编码过程中除 心理声学模型 其它的处理环节,如 瞬时噪声整形(TNS)、知觉噪声替换(PNS)、立体声编码(stereo) 等模块。
我觉得 时域信号 到 $\text{QMDCT}$系数 的过程, 本质就是 $\text{MDCT}$ 变换 加上 心理声学模型量化 。
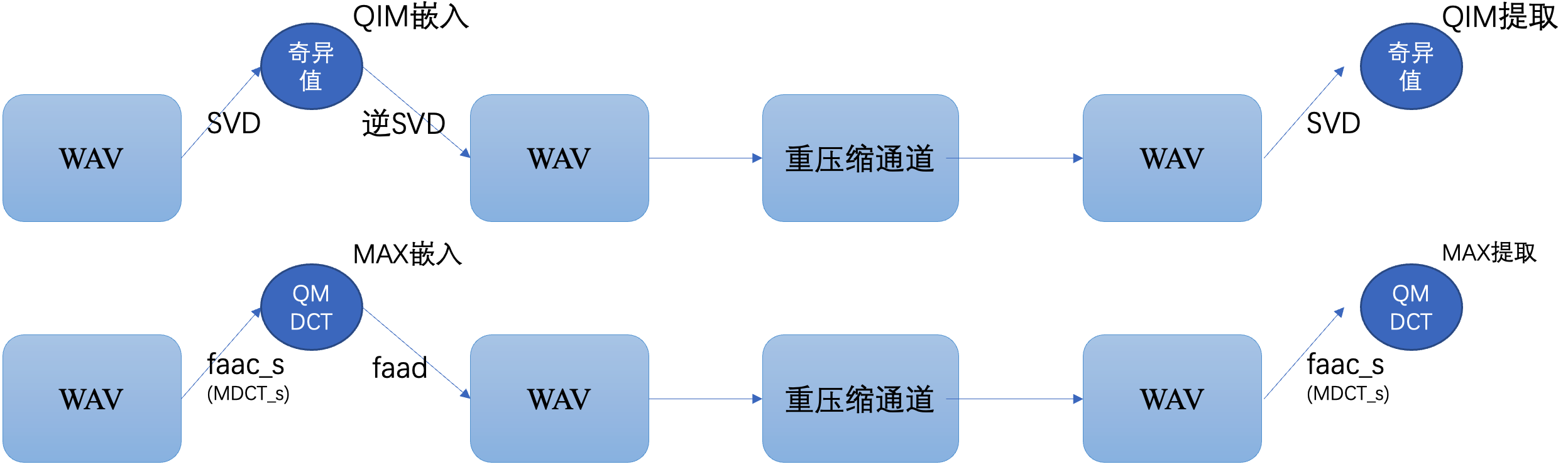
为了让 $\text{faac_s}$ 这个过程顺利的进行,更多的达到变换的目的而不是编码的目的,需要对一些编码的模块进行关闭。
块变换控制
--shortctl X Enforce block type (0 = both (default); 1 = no short; 2 = no long).- 瞬时噪声整形(TNS),$\text{faac}$ 默认就没开,我也没去动
知觉噪声替换(PNS),$\text{faac}$ 默认等级为 $4$,改成 $0$。(不会产生量化值)
--pns <0 .. 10> PNS level; 0=disabled. if (bandqual[sb] < pnsthr) { coderInfo->book[coderInfo->bandcnt] = HCB_PNS; coderInfo->sf[coderInfo->bandcnt] += lrint(log10(etot) * (0.5 * sfstep)); coderInfo->bandcnt++; continue; }联合立体声编码,$\text{faac}$ 默认为 $2$,改成 $0$。(对量化值会造成影响)
--joint 0 Disable joint stereo coding. --joint 1 Use Mid/Side coding. --joint 2 Use Intensity Stereo coding.
最终嵌入提取时必须额外给 $\text{faac}$ 提供的参数:
faac --shortctl 1 --pns 0 --joint 0 1.wav -o 1.aac
目的就是使 重压缩对音频造成的影响 在这种特殊的编码过程中不对 $\text{QMDCT}$ 系数造成 数量和频谱分布上 的影响。
$(3.2)$ 是否还有其它会影响 QMDCT变换编码的模块?
3.1.4 提取位置
可以考虑在 $\text{MDCT}$ 系数时候直接进行提取,当然也可以 $\text{QMDCT}$ 量化后再提取
可以进行试验测试结果,当前使用的是 $\text{QMDCT}$ 系数位置提取。
3.2 试验结果
测试样本:$100$ 个 $10s$ 的双通道 $44.1\text{kHz}$ 的 $\text{wav}$音频文件
3.2.1 嵌入容量
\[\frac{44100}{1024}\times 17 = 732(b/s)\]3.2.2 听觉扰动
$10s$ 嵌入了 $5000$ 比特,放弃了前 $100$ 帧
在基本满嵌入的情况下没有显著扰动,相对于 $\text{mp3}$ 的效果有显著的提升。(我的耳朵评测…)
3.2.3 误码率
一秒大约含有 $44100/1024=43$ 帧,$1000$ 比特需要 $1000/17=59$ 帧
$10s$ 嵌入了 $1000$ 比特,放弃了前 $100$ 帧,也就是在 $[101,159]$ 帧进行嵌入。
构建了三种重压缩流程
其中 $(faad)$ 和 $(lame)$ 是默认参数配置
- $wav\rightarrow(faac_{emb})\rightarrow aac_{se}\rightarrow(faad)\rightarrow wav_e\rightarrow(faac_{ext})$
- $wav\rightarrow(faac_{emb})\rightarrow aac_{se}\rightarrow(faad)\rightarrow wav_e\rightarrow(faac)\rightarrow aac_e \rightarrow(faad)\rightarrow wav_e\rightarrow(faac_{ext})$
- $wav\rightarrow(faac_{emb})\rightarrow aac_{se}\rightarrow(faad)\rightarrow wav_e\rightarrow(lame_{encode})\rightarrow mp3e \rightarrow(lame{decode})\rightarrow wav_e\rightarrow(faac_{ext})$
- $wav\rightarrow(faac_{emb})\rightarrow aac_{se}\rightarrow(faad)\rightarrow wav_e\rightarrow(SoundCloud_{encode})\rightarrow mp3e \rightarrow(lame{decode})\rightarrow wav_e\rightarrow(faac{ext})$
误码率结果
| 起始点 | 通道$1$ | 通道$2$ | 通道$3$ | 通道$4$ |
|---|---|---|---|---|
| $0$ 帧,$1000bit$ | $0.0274$ | $0.05614$ | $0.03286$ | |
| $100$ 帧,$1000bit$ | $0.00594$ | $0.03527$ | $0.01141$ | $0.01017$ |
| $100$ 帧,$5000bit$ | $0.00973$ | $0.03857$ | $0.01473$ |
- $100$ 帧比从 $0$ 帧好很多的原因是因为音频开始的时候容易有静音帧
- 误码率:通道$2(\text{faac})>$通道$3(\text{faac})>$通道$1(\text{base})$
- 为什么误码率$\text{faac}$通道会大于$\text{lame}$通道?
音频编码模块试验
- $\text{lame}$ 通道默认配置:$\text{stereo-MS}$
- $\text{faac}$ 通道默认配置:$\text{stereo-IS, PNS - level4, TNS - no}$
- 必然存在的:心理声学模型计算、长短块等
- 默认关闭或者可能存在的:预测、强调等
借助于 $\text{faac}$ 编码器的参数控制,我可以对一些模块进行消融试验:
长短块控制:
--shortctl X 强制块的类型
(0 = both (默认); 1 = no short; 2 = no long).
知觉噪声控制:
--pns <0 .. 10> PNS level; 0=disabled.
强度立体声编码控制:
--joint X
(0 = LR; 1 = MS; 2 = IS).
默认配置:$\text{长短块混合,pns=4,joint=IS,前17频带}$
| 参数配置 | 误码率 | 提升 |
|---|---|---|
| 默认配置 | $0.03527$ | |
| 仅长块 | $0.02614$ | $0.00913$ |
| 关闭PNS | $0.03763$ | $-0.00236$ |
| Joint=LR | $0.00784$ | $0.02743$ |
| Joint=MS | $0.01818$ | $0.01709$ |
| $[0,9]$频带 | $0.02814$ | $0.00713$ |
- 猜想长短块的使用在重压缩通道中对数值的影响并没有那么大?
- PNS造成的效果和静音帧类型
- 联合立体声编码影响很大,尤其是 $\text{IS}$(强度立体声这种编码方式)
3.3 讨论
3.3.1 静音帧

- 如果AAC进行AAC重压缩,静音帧是没有问题的,因为静音帧永远都是静音帧。
- 如果AAC转WAV,再进行MP3重压缩,上述解码方法会存在静音帧变非静音帧的情况。
同粒度大小变换
是否有稳定性特别强的帧选择策略?
3.3.2 单帧STC
因为误码率很低,而且容量大,是否可以考虑放弃一定的准确率使用STC减少扰动。虽然会增大误码率,当是可以再利用BCH把误码率降下去。
3.3.3 模块针对性优化
比如 $\text{Stereo_IS}$
3.3.4 MP3可复现
提前修改MDCT系数,反复预量化使得QMDCT成立
3.3.5 试验
网易云播客,喜马拉雅等
3.3.6 个人方向
- 声学方面具体模块
- 鲁棒性方向
文档信息
- 本文作者:Jiamin Zeng
- 本文链接:https://jiaminzeng.github.io/2022/11/21/Paper-%E9%9F%B3%E9%A2%91%E9%9A%90%E5%86%99/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)